Controlling multi-species population dynamics
- Funding: partially funded by German Research Foundation, grant SA 847/22-2.
- PIs and collaborators: Oliver Sawodny (University of Stuttgart), Miroslav Krstić (UC San Diego).
🔗 Related Publications
See Control Theory Publications
Populations (in ecology, epidemics, biotechnology, economics, social processes) do not only interact over time but also age over time. It is therefore common to model them as age-structured partial differential equations, where age is the ‘space variable’. Since the models also involve integrals over age, both in the birth process and in the interaction among species, they are in fact integro-partial differential equations (IPDEs) with positive states and inputs, turning them into an extremely challenging control problem.
Our works revolve around the fact that the considered familiy of IPDE systems can be transformed into a system of two coupled ordinary differential equations (ODE) and two autonomous, exponentially stable integral delay equations (IDE).
Predator-Prey Dynamics
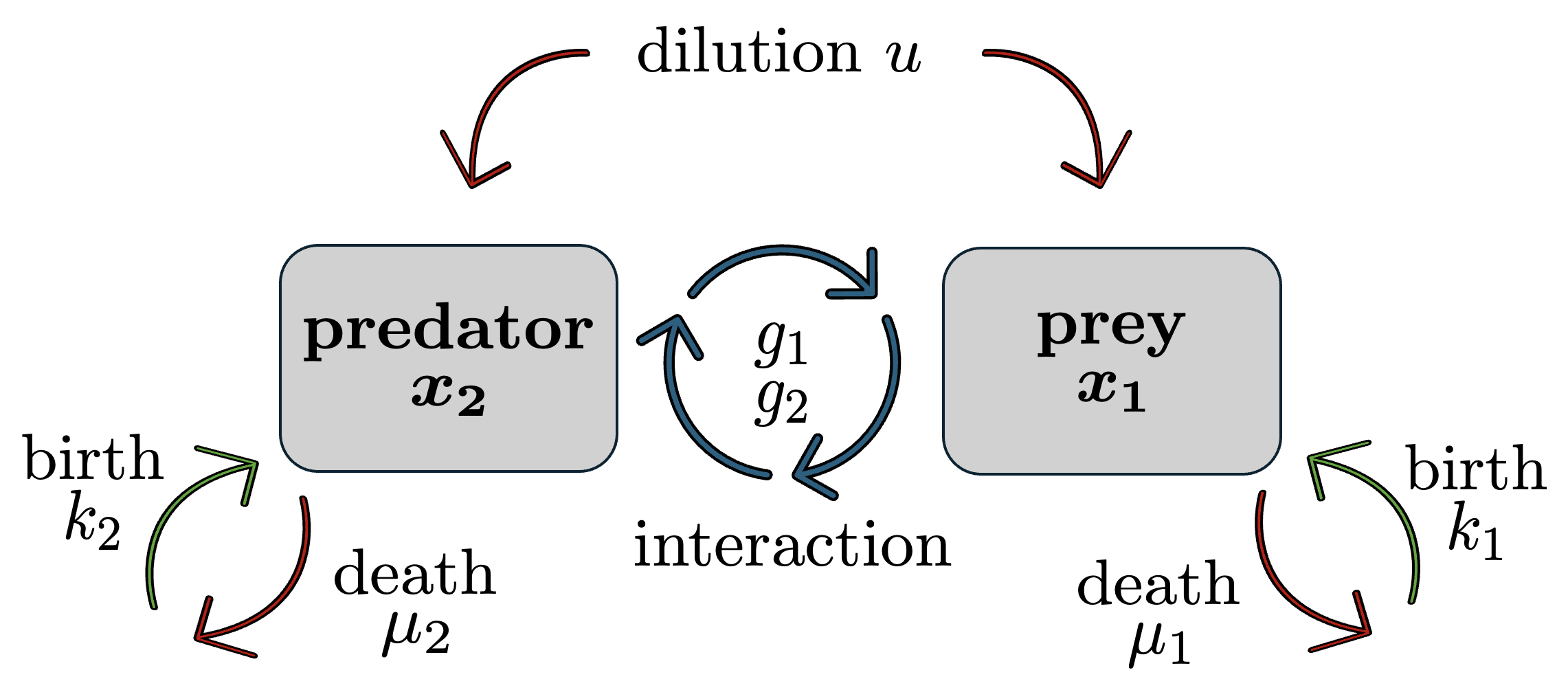
With a modified Volterra-like control Lyapunov function,
- We design a simple feedback which employs possibly negative harvesting for global stabilization of the ODE model, while guaranteeing regional regulation with positive harvesting.
- Extending this to a more sophisticated, restrained controller we achieve regulation for the ODE model globally, with positive harvesting.
- For the full IPDE model, with the IDE dynamics acting as large disturbances, for both the simple and saturated feedback laws we provide explicit estimates of the regions of attraction.
Predator-Predator Dynamics
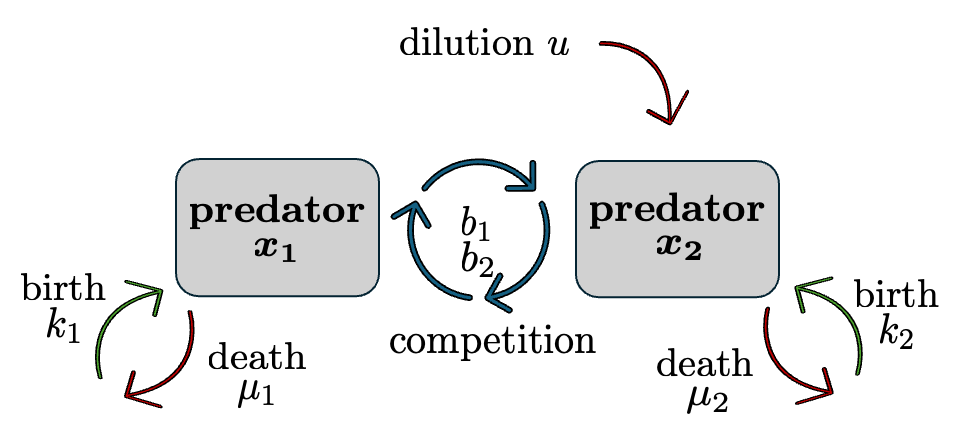
Using backstepping,
- The ODEs are globally stabilized.
- An estimate of the region of attraction of the asymptotically stabilized equilibrium of the full IPDE system is provided, under a positivity restriction on control.
📄 As of June 2025, results have just been submitted to automatica, and we are waiting for a decision notification from CDC 2025.
Last updated: June 2025
